| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- JavaScript
- sass
- express
- 자바스크립트
- mapGetters
- scss
- 쉬운설명
- 자료구조
- TypeScript
- Vue
- jsx
- react
- input
- ES6
- HOC
- CSS
- Vue transition
- 댓글달기
- storybook
- Vue.js
- nodejs
- MySQL
- v-html
- event
- vuex
- State
- Wecode
- App.vue
- webpack
- 리액트
- Today
- Total
익명의 개발노트
[Non-Linear] Graph 구조 본문
1. Graph란?
1) 모든 노드를 각각 노드와 연결하는 선(E, edge)을 하나로 모아 놓은 자료 구조
2. 종류
1) 방향 그래프(directed)
2) 무방향 그래프(undirected)
3) 가중치 그래프(weighted or Network)
3. 특징
1) 그래프에는 방향이 있을 수도, 없을 수도 있다.
2) 그래프에는 사이클이 존재 할수도, 존재 하지 않을 수도 있다.
3) 그래프는 네트워크 모델이다.
4) 2개 이상의 경로가 가능하다.
5) Root Node의 개념이 없다.
6) 부모-자식 개념이 없다.
7) self loop 뿐만 아니라 loop or circuit 모두 가능하다.
8) 순회는 DFS 또는 BFS로 이루어진다.
9) 그래프는 순환(Cyclic) 혹은 비순환(Acyclic)이다.
4. 표현방법
1) 인접리스트(Adjacency list)
2) 인접행렬(Adjacency matrix, 2차 행렬)
5. 설명
1) 인접리스트
(1) 그래프 표현시 가장 일반적인 방법
(2) 배열의 각 인덱스마다 Linked list를 통해서 표현가능하다.
(배열에 모든 노드를 넣고, 노드와 연결된 노드를 Linked list 방식으로 저장한다)
0: 1
1: 2
2: 0, 3
3: 2
4: 6
5: 4
6: 52) 인접행렬
(1) 2차 배열로 표현하며, 연결되어있으면 1, 아니면 0으로 표기한다.
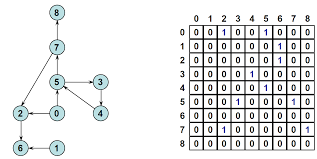
6. 그래프 검색(탐색) 방법
1) 종류
(1) 깊이우선검색(DFS, Depth First Search)
(2) 넓이우선검색(BFS, Breath First Search)
2) 설명
(1) 깊이우선검색(DFS, Depth First Search)
가. 트리구조 순회방법에서 사용된 In-order, Pre-order, Post-order가 DFS 검색에 속한다.
나. Root Node 혹은 다른 Node에서 시작해서 child Node가 끝날때까지 child Node를 검색하고, childe Node가
끝나면, 위로 올라가 sbling Node를 동일한 방법으로 검색하는 방법임.
다. 말그대로 깊게 탐색한다는 의미.
라. 구현은 스택을 이용해서 구현.
(2) 넓이우선검색(BFS, Breath First Search)
가. Root Node 혹은 다른 Node에서 시작해서 Child Node를 먼저 검색하고, 검색이 끝나면 Child Node의
Child Node를 검색하는 방법으로 넓게 검색함.
나. 구현은 큐를 이용해서 구현.

7. 그래프
1) Dictionary를 만들어서 활용하자.
function Dictionary(){
var items = {};
this.set = (key,value) => {
items[key] = value;
}
this.get = (key) => {
return this.has(key) ? items[key] : undefined;
}
this.delete = (key) => {
if(this.has(key)){
delete items[key];
return true;
}
return false;
}
this.has = (key) => {
return key in items;
}
this.values = () => {
var values =[];
for(var k in items){
if(this.has(k)){
values.push(items[k]);
}
}
return values;
};
this.keys = function(){
return Object.keys(items);
}
this.getItems = function(){
return items;
}
} 2) 순수 그래프 구현
function Graph(){
var vertices = []; //Graph의 점들의 이름을 배열에 저장.
var adjList = new Dictionary(); // 인접리스트를 저장하기 위해 Dictionary를 사용. Dicrionary는 키갑으로 vertex의 이름을, 인접리스트 vertex의 값을 벨류값으로 사용한다.
//private 속성.
this.addVertex = function (v) {
vertices.push(v);
adjList.set(v, []);
}
//undireact 기준으로 설명
this.addEdge = function(v,w){
adjList.get(v).push(w); //다이렉트면 이거 하나만으로도 충분함.
adjList.get(w).push(v);
}
//화면에 도식.
this.toString = function(){
var s = '';
for(var i=0; i<vertices.length; i++){
s += vertices[i] + ' → ';
var neighbors = adjList.get(vertices[i]);
for(var j=0; j<neighbors.length; j++){
s += neighbors[j] + ' ';
}
s += '\n';
}
return s;
};
}
var graph = new Graph();
var myVertices = ['A','B','C','D','E','F','G','H','I'];
for(let i=0; i<myVertices.length; i++){
graph.addVertex(myVertices[i]);
}
graph.addEdge('A',"B");
graph.addEdge('A', 'C');
graph.addEdge('A', 'D');
graph.addEdge('C', 'D');
graph.addEdge('C', 'G');
graph.addEdge('D', 'G');
graph.addEdge('D', 'H');
graph.addEdge('B', 'E');
graph.addEdge('B', 'F');
graph.addEdge('E', 'I');
console.log(graph.toString());
//결과값
A → B C D
B → A E F
C → A D G
D → A C G H
E → B I
F → B
G → C D
H → D
I → E
3) BFS 구현
function Graph(){
...
//1.queue Q를 만든다.
//2. 시작점 v를 회색으로 칠하고 Q에 넣는다.
//3 반복문을 돌리는 동안 Q가 빈 vertex가 아니면,
// 3-1) Q에서 u를 뺸다.
// 3-2) u를 회색으로 칠한다.
// 3-3) 방문하지 않은 모든 하얀색 점들을 Enqueue한다.
// 3-4) u를 탐색하고 검정색으로 칠한다.
//초기 셋팅. 흰색 : 방문, 탐색안한 점, 회색 : 방문만 한 점, 검정 : 둘다 한점.
var initializeColor = function(){
var color = [];
for(var i=0; i<vertices.length; i++){
color[vertices[i]] = 'white'; //모든 점 흰색으로 시작.
}
return color;
};
this.bfs = function(v, callback){
var color = initializeColor(),
queue = new Queue(); //큐 생성
queue.enqueue(v); // 시작점 넣기.
while(!queue.isEmpty()){ // 큐가 비어있지 않으면.
var u = queue.dequeue(), //큐로부터 제거.
neighbors = adjList.get(u);
color[u] = 'grey';
for(var i=0; i<neighbors.length; i++){
var w = neighbors[i];
if(color[w] === 'white'){
color[w] ='grey'; //아직 방문안한 점들을 회색으로
queue.enqueue(w);
}
}
color[u] = 'black' //탐색끝나면 검정
if(callback){
callback(u);
}
}//while end
}
}
...
function printNode(value){
console.log("Visited vertex : "+ value);
}
graph.bfs(myVertices[0],printNode);
'Visited vertex : A'
'Visited vertex : B'
'Visited vertex : C'
'Visited vertex : D'
'Visited vertex : E'
'Visited vertex : F'
'Visited vertex : G'
'Visited vertex : H'
'Visited vertex : I'4) 최단거리 BFS
function Graph(){
...
//최단거리
this.BFS = function(v){
var color = initializeColor(),
queue = new Queue(), //큐 생성
d = [], // 시작점부터 어느점까지의 거리
pred = []; //최단경로 구하는 전처리기.
queue.enqueue(v); // 시작점 넣기.
for (var i=0; i<vertices.length; i++){ //{3}
d[vertices[i]] = 0; //{4}
pred[vertices[i]] = null; //{5}
}
while(!queue.isEmpty()){
var u = queue.dequeue(),
neighbors = adjList.get(u);
color[u] = 'grey';
for(i=0; i<neighbors.length;i++){
var w = neighbors[i];
if(color[w] === 'white'){
color[w] = 'grey';
d[w] = d[u] +1;
pred[w] = u;
queue.enqueue(w);
}
}
color[u] = 'black';
}
return {
distances : d,
predecessors : pred
};
}
}
var shortestPathA = graph.BFS(myVertices[0]);
console.log(shortestPathA);
//결과
{ distances: [ A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2, I: 3 ],
predecessors:
[ A: null,
B: 'A',
C: 'A',
D: 'A',
E: 'B',
F: 'B',
G: 'C',
H: 'D',
I: 'E' ] }'프로그래밍 관련자료 > 자료구조 및 Big-O' 카테고리의 다른 글
| [Non-Linear] Hash Table (0) | 2019.04.21 |
|---|---|
| [Linear] Doubly linked list (0) | 2019.04.19 |
| [Non-Linear] Binary - heap (0) | 2019.04.15 |
| [Non-Linear] 트리구조 순회방법(Tree traversals) (0) | 2019.04.15 |
| [Non-Linear] 트리구조 (0) | 2019.04.15 |




